Intro
I recently had to generate a random 2D heightmap for a spare time project.
Then I recalled Paul Bourke excellent page about fractals (and a lot more !)
You will find a great article on how to generate 3D planets with a very simple algorithm here. In an ancient time I implemented this algorithm in a 3DS Max plugin. And today I thought it would be funny to transpose it to 2D and see what happens …
Let me quickly describe the 3D algorithm in a few steps:
- Start with a sphere
- Pick a random plane (actually you need a normal to that plane)
- Increase height on one side and decrease height on the other side of the plan
- Go back to step 2
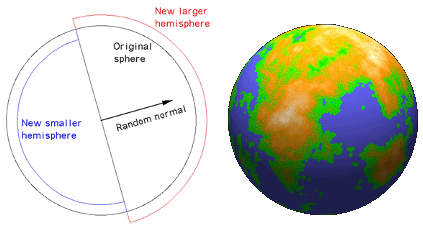Illustrations from Paul Bourke (1000 iterations)
2D Transposition
Let’s now talk about how we can transpose this algorithm to 2D:
- Start with a flat map (square or rectangular)
- Pick a random line that cut the map (you need two points or a point and a normal)
- Randomly increase height on one side of the line and decrease height on the other side
- Go back to step 2.
Some results after 10000 iterations on a 512x512 grid (12s on my core i7)
Indeed the more iteration the more “details” you get but the downside is that it takes longer to generate (for each iteration all pixels are evaluated). Then I had the idea to try a different workflow:
- Pick a random “normal” associated with a random height offset and save it
- Go back to step 1 as many times as number of iteration
- For every pixel sum the height offset given by each line
I naively I though it would be faster, but indeed it produce exactly the same amount of processing. There is at least one benefit to this method, being able to calculate elevation for any coordinate (the map size can grow at any time).
Generalization
After playing a bit with my generator, I thought it could funny to go a bit further. What happens if instead of dividing the map in two part with a line, I choose a different primitive like a circle.
And well, why not a triangle or square?
Here are some outputs using a random combination of lines, circles, triangles and rectangles. As you can see other shapes introduce a huge bias, most probably because I use circles, rectangles and triangles that fully lie inside the grid. I will try to find a better way to define those shapes. But the good thing it that it seems to remove visible line patterns (that what led me to this idea).
Updated (September 30th 2014)
At the cost of a lot more iterations, and using a square grid instead of a rectangular one the visual results seem good. The performance are not so good even with a small change I did to take advantage of parallel computing (4x times faster on a quad core).
Parallel.ForEach(
(from x in Enumerable.Range(0, this.width)
from y in Enumerable.Range(0, this.height)
select new Tuple<int, int>(x, y)),
p => this.map[p.Item2, p.Item1] = this.dividers.Sum(s => s.GetValue(p.Item1, p.Item2)));
I didn’t understood it first, but using a rectangular grid introduce a small bias in the density of horizontal and vertical lines that was generating more visible line patterns.
In the end I’m a bit disappointed by the visual results. Indeed increasing the number of iterations to 1000 reduce artifacts at the cost of generation time.
Below you will find a piece of code from a visual studio demo project:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Threading.Tasks;
using System.Windows;
namespace HeightMapDemo
{
public class PaulBourke
{
private interface IDivider
{
double GetValue(double x, double y);
}
private class Splitter : IDivider
{
public Splitter(Point a, double va, Point b, double vb)
{
this.X = (int)a.X;
this.Y = (int)a.Y;
this.va = va;
this.vb = vb;
this.ratio = (b.X - this.X) / (b.Y - this.Y);
}
private readonly int X;
private readonly int Y;
private readonly double va;
private readonly double vb;
private readonly double ratio;
public double GetValue(double x, double y)
{
return this.ratio * (y - this.Y) - (x - this.X) > 0 ? this.va : this.vb;
}
}
private readonly Random randomizer;
private readonly int width;
private readonly int height;
private readonly double[,] map;
private IDivider[] dividers;
public PaulBourke(Random randomizer, int width, int height)
{
this.randomizer = randomizer;
this.width = width;
this.height = height;
this.map = new double[height, width];
this.Iterations = 10000;
}
public int Iterations { get; set; }
public double[,] Map
{
get { return this.map; }
}
public IEnumerable<double> Map1D
{
get { return this.map.Cast<double>(); }
}
public void Generate()
{
this.Prepare();
Parallel.ForEach(
(from x in Enumerable.Range(0, this.width)
from y in Enumerable.Range(0, this.height)
select new Tuple<int, int>(x, y)),
p => this.map[p.Item2, p.Item1] = this.dividers.Sum(s => s.GetValue(p.Item1, p.Item2)));
}
private void Prepare()
{
this.dividers = new IDivider[this.Iterations];
Parallel.ForEach(Enumerable.Range(0, this.Iterations),
i => this.dividers[i] = this.CreateSplitter());
}
private IDivider CreateSplitter()
{
int sideA = this.randomizer.Next(4);
Point pointA = this.PickPointOnSide(sideA);
int sideB = this.Next(4, sideA);
Point pointB = this.PickPointOnSide(sideB);
while (pointB == pointA)
{
pointB = this.PickPointOnSide(sideB);
}
double valueA = 2 * this.randomizer.NextDouble() - 1d;
double valueB = -valueA;// this.randomizer.NextHeight();
return new Splitter(pointA, valueA, pointB, valueB);
}
private Point PickPointOnSide(int side)
{
Point p = new Point();
switch (side)
{
case 0:
p.Y = 0.0;
p.X = this.randomizer.Next(this.width);
break;
case 1:
p.Y = this.randomizer.Next(this.height);
p.X = this.width;
break;
case 2:
p.Y = this.width;
p.X = this.randomizer.Next(this.width);
break;
case 3:
p.Y = this.randomizer.Next(this.height);
p.X = 0.0;
break;
}
return p;
}
private int Next(int maxValue, int except)
{
int value = this.randomizer.Next(maxValue);
while (value == except)
{
value = this.randomizer.Next(maxValue);
}
return value;
}
}
}
Updated (October 3rd 2014)
Fuzzyness
I was wondering how I could achieve good results with less iterations. Because I must admit that less 5K iterations produces visible edges (even if I mix different primitives). Then I though that instead of splitting the grid with hard edges I could introduce “fuzzy” edges.
How I made it ? Using perlin noise to scramble edges. Basically if a point is close enough to an edge, instead of being binary categorized, a 2D perlin noise is used to categorize. Below you can see the code for a line divider:
public override double GetValue(Point p)
{
Vector v = this.origin - p;
if (this.UseEdge)
{
return Math.Abs(v.X * this.normal.X + v.Y * this.normal.Y) < 0.5 ? 10d : 0d;
}
double distance = v.X * this.normal.X + v.Y * this.normal.Y;
if (this.Fuzziness > 0 && Math.Abs(distance) < this.Fuzziness)
{
double generate = this.Fuzziness*this.PerlinNoise.Generate(p.X, p.Y);
return generate > distance ? this.va : this.vb;
}
return distance < 0 ? this.va : this.vb;
}
In the code above you can see:
- a toggle to display only the line itself
- the line is defined by its normal and a point on the grid
- the distance is actually the result of a dot product
- if the point is in the fuzziness area then “randomize” using perlin noise the point value.
This algorithm seems to remove hard edges artifacts but, well introduce other kind of artifacts (depending on the perlin noise parameters). But here is a nice result with less than 1000 iterations:
